A los profes de Matemáticas nos encanta comenzar las clases planteando un pequeño reto para despertar las mentes. Uno de mis favoritos es el problema de Monty Hall.
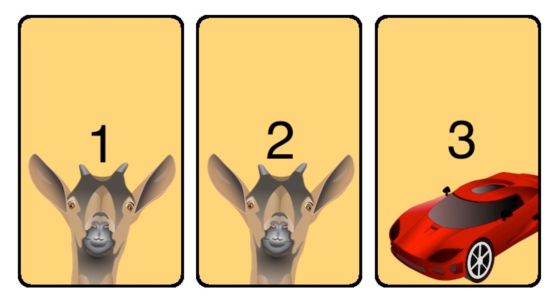
Os pongo en situación: En un concurso de la tele, has derrotado a tus contrincantes y te encuentras ante la prueba final. El presentador te coloca frente a tres puertas (A, B y C, por ejemplo). Detrás de dos de ellas hay un premio absurdo -originalmente era una cabra-; detrás de la otra, un coche.
Te piden que elijas una de ellas e imaginemos que eliges la puerta A. Entonces, el presentador, que sabe exactamente qué hay detrás de cada puerta y quiere darle emoción a la audiencia, abre una de las otras dos para eliminarla. En ella (imaginemos que era la puerta C), por supuesto, había una cabra. El coche, por tanto, está en tu puerta, la A, o en la otra, la B. En ese momento te pregunta si te quedas con la puerta que elegiste en un principio o prefieres cambiar y elegir la otra. Tensión máxima.
¿Qué harías tú?
Este problema lo planteó la matemática Marilyn vos Savant. El nombre del problema, Monty Hall, hace referencia al nombre del presentador de un concurso de la tele estadounidense de los años 70 llamado algo así como “hagamos un trato”. Parece ser que en el programa ocurría algo similar a lo expuesto. La solución que propuso Savant no gustó nada a los lectores de la revista donde se publicó. De hecho, recibió cientos de cartas poniéndola a caldo y cuestionando sus conocimientos matemáticos por afirmar tal barbaridad. La mayoría de ellos, como yo en su momento, y probablemente tú que estás leyendo esto, pensó que, al quedar dos puertas, A y B, las probabilidades de que el coche esté en la tuya son del 50%. Es algo intuitivo al tener dos opciones. El problema está en olvidar que, cuando elegiste, tus opciones de acertar no eran esas, sino algo menores.
Elijas lo que elijas de entrada, el presentador sabe dónde está el coche y tiene que abrir una puerta en la que, obligatoriamente, va a descubrir una cabra. Analiza conmigo las posibilidades eligiendo la puerta A:

Cuando compramos lotería, pensamos que a alguien le tiene que tocar, y ese alguien puedes ser tú; lo que no queremos pensar es en las decenas de miles de personas a las que no les va a tocar nada, pues como lo pensemos mucho no compramos el boleto. Al plantear las probabilidades de que algo ocurra, solemos centrarnos en nuestras opciones de éxito y no en las de fracaso.
En el momento de elegir por primera vez, todas las puertas tienen un 33% de posibilidades de ser la del coche. Si al elegir una, piensas que hay un 66% de posibilidades de que el coche esté en otra puerta distinta, a lo mejor empieza a sonarte atractiva la idea de cambiar. Cuando el presentador desvela una de ellas, la puerta eliminada pasa de tener un 33% de posibilidades, a tener un 0%; las probabilidades de la puerta eliminada se pasan a la otra, que aumenta a un 66%.
Se ve mucho más claramente suponiendo que hubiera 100 puertas en vez de solo tres: En una hay un coche y en el resto, cabras. Eliges una. Tus probabilidades de acierto son de un 1%; las de error son del 99%. El presentador abre todas las puertas salvo la tuya y otra; el coche está entre una de esas dos. ¿Confiarías en tu puntería inicial? Yo, ahora, cambiaría.
Tras la explicación, imagino que muchos de los que tachaban a Savant (por cierto, según el Guiness de los Records, la persona con mayor cociente intelectual del planeta) de ser más bruta que un bocadillo de escombros, se disculparían.
Una vez que lo comprendes y dices ese clásico “¡ahhh!”, tu perspectiva cambia. No obstante, cada vez que lo cuento en clase, mis alumnos, lo comprendan o no, siempre me dicen lo mismo:
-Profe, a mí ganar el coche me da igual; yo prefiero una cabra.
Ángel Marcos.
Profesor Primaria